What Is The Factorial Of Hundred?
One of the most fascinating concepts in mathematics is that of the factorial. It combines simple calculations to produce results of amazing magnitudes, leading down an incredible rabbit hole of assertions and computations. A clear manifestation of this is the hundred factorial, often written as 100!– a number so huge that it pushes the boundaries of computational abilities.
When we talk about factorials, we enter the realm of big numbers, large calculations, and a world of real-life implications. Can you imagine that something as straightforward as counting and sequential calculations can unleash such potential? That’s the miracle of factorials. At the heart of this article lies the extraordinary question: “What is the factorial of 100?”
To address this, we will first aim to understand the concept and calculations behind factorials. Following this, we’ll shed light on the real-world examples of factorials. Who knew that simple calculations could have such profound implications? Next, armed with the understanding of factorials, we will glide through the process to calculate the factorial of 100, a giant of a number that will leave you marveling at the power of maths. We will supplement this with useful tips on dealing with such voluminous calculations, all the while navigating the common pitfalls.
Stick around to discover the magic that the hundred factorial unfolds, and immerse yourself in the charm of factorials!
What is a factorial?
In elementary mathematics, a factorial represents the product of all positive integers less than or equal to the involved number. The concept of a factorial is primarily used in permutations and combinations, which are core elements of probability theory. A number’s factorial is represented with the symbol !. Therefore, when you read n!, it’s referred to as ‘n factorial.’
How is a factorial calculated?
Calculating a factorial can involve simple multiplication if we are dealing with small numbers. For instance, consider the factorial of 4. It can be calculated in the following manner: 4! = 4 x 3 x 2 x 1 = 24.
It’s clear from our example that calculating the factorial of a number involves gradually reducing the number by 1 and incorporating it into the ongoing product until you reach 1.
What is the factorial of 100?
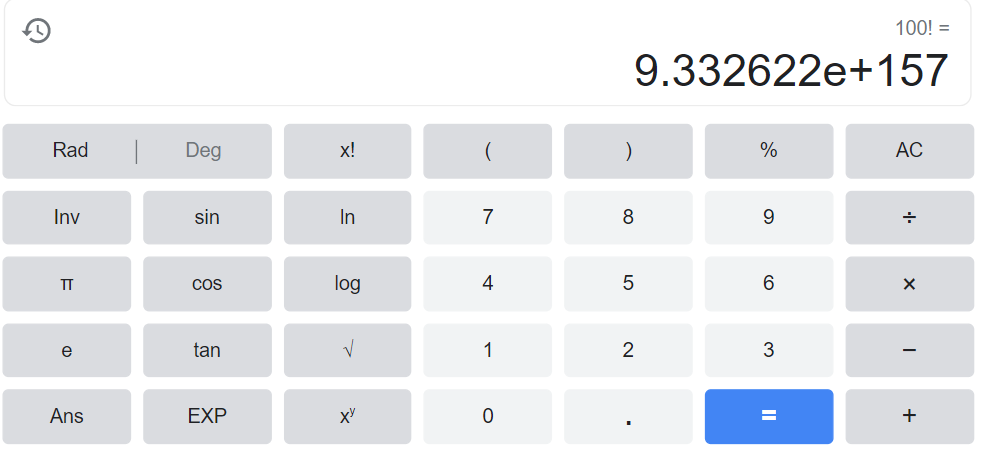
The factorial of 100 or 100! is an enormous number, so large, in fact, that most standard calculators can’t handle its computation. But done using advanced computational tools, it’s found to be approximately 9.33262154439441e+157. That is, it’s a number with 158 digits! It’s a pretty large number, isn’t it?
Real-world examples of factorials
Factorials are not just exclusive to mathematics textbooks. They have tangible utility in various real-life applications. From organizing and partitioning objects, finding out permutations and combinations in probability, and even in encoding data in Computer Science, factorials find significance across various fields.
Calculating the factorial of 100
Simply jotting down the value might suffice, but how was this huge value for the factorial of 100 actually computed? Unfortunately, conventional calculators tend to falter due to the massive quantity of the result. However, several computer programs and mathematical software, such as Wolfram Alpha or Mathematica, are up to the task.
Step-by-step instructions on how to calculate the factorial of 100 using a calculator and by hand
Although manually calculating the factorial of 100 is a daunting task, you can symbolically represent it as follows:
100! = 100 x 99 x 98 x ... x 3 x 2 x 1.
While doing this by hand might be unmanageable for most, computing it through software involves executing a loop that multiplies integers from 1 to 100.
For a standard scientific calculator, there’s usually a special function for calculations of factorials, symbolized as x! or n!; however, it’s important to bear in mind that such calculations might be limited by the calculator’s capacity.
Tips for calculating large factorials
For large factorial calculations, it’s generally best to resort to calculators with large-integer support or suitable software.
Common mistakes to avoid when calculating factorials
Two common errors occur when dealing with factorials:
- Neglecting that the factorial of zero:
0!is 1, not 0. - FORTRAN language users often use an exclamation mark (!) for comments, which may cause confusion with the factorial symbol.
How factorials are used in probability and statistics
Factorials play an important role in statistics and probability, especially in combinations and permutations.
How factorials are used in computer science
In computer science, factorials can be found in algorithms, particularly those relating to sorting and data structure traversal. They also underpin the O(n!) complexity found in some algorithms.
Other interesting real-world applications of factorials
Factorials are also utilized in Google PageRank algorithm, signal processing, bioinformatics, and even in arranging seating plans!
History of factorials
The concept of factorial was introduced by Swiss mathematician Leonhard Euler in the 18th century, who extended its usage from integers to real and complex numbers, part of what we now call the gamma function.
Other factorial functions
There are also other factorial functions, such as the double factorial and the subfactorial, that serve different mathematical purposes. For instance, the double factorial is the product of a number with all numbers of the same parity that are smaller, while the subfactorial, symbolized as !n, denotes the derangements (permutations where no element appears in its original position) of a set.
Fun facts about factorials
Did you know that the number of zeros at the end of 100! is 24? Or that the sum of the digits in 100! is 648?
Conclusion
To recap, the factorial of 100, a whimsically large number, is central to various mathematical and practical computations. Factorials, introduced by Euler, have expanded in their application beyond mere mathematical curiosity, encompassing fields like computer science, bioinformatics, probability, and statistics.
The factorial function has seen an expansion to include other types, namely double factorial and subfactorial, which situate themselves differently in mathematical usage. Although calculating large factorials like that of a hundred might seem intimidating at first, it becomes quite manageable with an appropriate understanding and useful computational tools.
It’s fascinating to observe how such a seemingly simple concept can scale to such enormous magnitudes and how mathematics continues to furnish tools to accommodate this growth. Factorials underpin many hierarchical and computational structures, and behold, the factorial of a hundred, this gigantic number, is a testament to the layered complexity hidden beneath simple mathematical operations.
While the magnitude of the factorial of a hundred is mind-boggling, there is a certain beauty in the manageability of its otherwise overpowering size, a tribute to the incredible agility and versatility of number systems and mathematical functions. The factorial function’s adaptability to real and complex numbers, among other expansions, showcases the fluid boundaries of mathematical principles, being able to shape-shift as needed to cater to escalating magnitudes or diversifying applications. After all, isn’t that what makes mathematics awe-inspiring?
The factorial of a hundred stands as a sentinel, at the crossroads of simplicity and complexity, of manageable calculations and colossal numbers, of theory and practice, inviting us to explore more, unravel further, and keep the flag of curiosity fluttering high.
FAQs
- What does 100 factorial mean?
100 factorial, written as 100!, refers to the product of all positive integers from 100 to 1. In other words, 100! = 100 x 99 x 98 x … x 3 x 2 x 1. It’s an impressive large number that entails 158 digits!
- What are some real-world applications of factorials?
Factorials offer tremendous utility across diverse fields. From computer algorithms and data structures to organize objects, probability, bioinformatics, and signal processing, factorials find widespread use.
- How do I calculate large factorials like 100 factorial?
Calculating large factorials manually can be extraordinarily cumbersome. Most calculators can’t handle such a large operation. However, programming languages (like Python or JavaScript) or mathematical software like Wolfram Alpha or Mathematica can efficiently compute such large numbers.
- What is the history of factorials?
The concept of factorials was introduced by the Swiss mathematician Leonhard Euler in the 18th century. Euler extended its usage from integers to real and complex numbers, which is part of what we now call the gamma function.
- Are there other types of factorials?
Yes, other types of factorials include the double factorial and subfactorial that have different mathematical function and usage. For instance, a double factorial is the product of a number with all numbers of the same parity that are smaller, while a subfactorial, denotes derangements.




