Trigonometry: Table, Functions and Formulas

Have you ever wondered how scientists found out the size of the Moon without actually measuring it, and way before Neil Armstrong landed on it? Or, have you questioned, how did the captains of the ships, in the past, figure out the distance of an island from an unknown point in the sea using sextant? Well, it was Trigonometry that came to their aid.

Today, we will discuss Trigonometry and let you know the various Trigonometry formulas that form the crux of the topic.

What is Trigonometry?

Contents show

Trigonometry is an important and fascinating branch of mathematics that has many practical uses. Very often, it is impossible or extremely difficult to find certain measurements. Using trigonometry, we can calculate distances, heights, and angles.

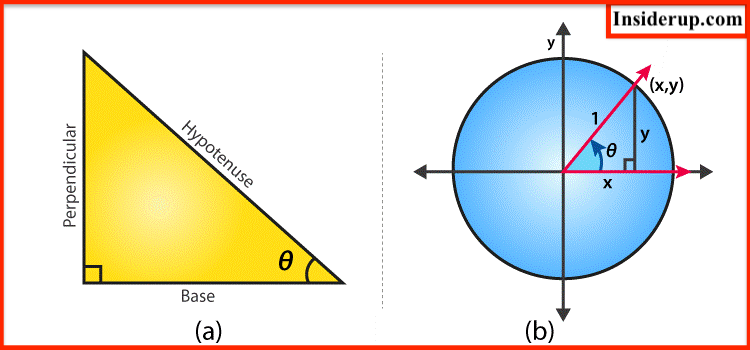
Fig. 1

Fig. 2

Hipparchus (190-120 BC), a Greek mathematician, is considered the Father of Trigonometry. In 140 BC, he was known to have prepared the trigonometric tables of chords in astronomy. The Table of Chords consists of angles in a circle of radius. Hipparchus tabulated every ½ degree to 180 degrees.

In the 16th century, the word “Trigonometry” was coined. It combines two Latin words – “trigonon” or triangle, and “metron”, meaning to measure. The field emerged in the Hellenistic world during the 3rd century BC, from applications of geometry to astronomical studies.

The Persian mathematicians in the Medieval Period developed trigonometry as a separate field of mathematics and developed trigonometric (or circular) functions in the 1500s. Interestingly, even the 4000-year-old stone tablets indicate that the ancient Babylonians and Egyptians used Trigonometry way back in the 1400s BC.

However, trigonometry is inseparably linked to the ancient Greek mathematician, and philosopher Pythagoras of Samos, believed to have been born in 580 BC. Pythagoras’ Theorem states that: In a right angle triangle, the sum of the squares of the sides is equal to the square of the hypotenuse, as shown in the figure:

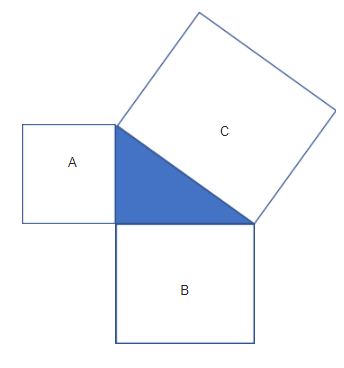Fig. 3

According to Pythagoras Theorem, the sum of the Square A and B is equal to Square C.

This relationship remains constant in a right triangle.

Trigonometry helps us apply the constant relationships between the sides and angles in a right triangle to calculate unknown distances, heights or angles. Many real-life situations are modelled by trigonometric functions, such as sea levels as the tide changes and day length as the seasons change.

Lets us take a simple example to understand how the Pythagoras Theorem works.

Tow similar right-angled triangles (Figure 4) with sides measuring

1st triangle – 3 inches, 4 inches and 5 inches

2nd triangle – 6 inches, 8 inches and 10 inches

Note that, since both the triangles are similar, their corresponding angles in equal.

Now,

(3 x 2) + (4 x 2) = (5 x 2)

And ,

(6 x 2) + (8 x 2) = (10 x 2)

When you solve the equation, the result clearly shows that the 1st triangle is exactly half the size of the 2nd triangle.

Fig. 4

It proves that two similar right-angled triangles maintain the ratio, as shown in Fig. 5.

You may work on any number of cases, and the ratio will not change.

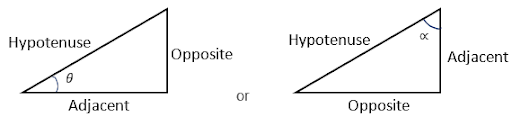
Fig. 5

Corresponding angles are the same.
Corresponding sides are in exact proportion.
The hypotenuse is always on the longest side and is proportional.

That means,

Sine is the ratio of opposite divided by the hypotenuse.
Cosine is the ratio of adjacent divided by the hypotenuse.

This relationship is as follows (Fig. 6):

Fig. 6

The ratio between sine, cosine and tangent will not vary.

Sine = Opposite/Hypotenuse
Cos = Adjacent/Hypotenuse
Tan = Opposite/Adjacent

If we apply these to the 1st triangle with 3 inches, 4 inches and 5 inches

Sine = 3/5 = 0.6
Cos = 4/5 = 0.8
Tan = ¾ = 0.75

We can take any two similar right-angled triangles, and provided we maintain the proportion of the sides, and when the angles are the same, we will prove it again and again.

As,

Sine = Opposite/Hypotenuse
Cos = Adjacent/Hypotenuse
Tan = Opposite/Adjacent

We can tabulate the formulas as follows.

Sine	Cos	Tan
Opposite	Adjacent	Opposite
Hypotenuse	Hypotenuse	Adjacent
Cos	Sec	Cot

The Trigonometric Ratio could be given as

Sine = 1/Cos
Cos = 1/Sec
Tan = 1/ Cot
Tan = Sine/ Cos
Cot = Cos/Sine

Note the Even and Odd Functions:

Even Functions	Odd Functions
Cos(-x) = Cos x	Sone(-x) = -Sine x
Sec(-x) = Sec x	Cosec(-X) = -Cosec x
	Cot(-x) = -Cot x
	Tan(-x) = – -Tan x

Since, Trigonometric Functions are periodic functions, they are:

Periodic Functions

sin(x 2nπ) = sin x

cos(x 2nπ) = cos x

tan(x nπ) = tan x

cot(x nπ) = cot x

csc(x 2nπ) = csc x

sec(x 2nπ) = sec x

*Where ‘n’ is an integer

Pythagorean Identities:

There are 3 main Identities, and they are very important to be remembered-

Sine^2 x Cos^2 x = 1
1 Tan^2 x = Sec^2 x
Cosec^2 x = 1 Cot^2 x

Identities – Sum and Differences:

Sine (x y) = Sine(x) x Cos(y) Cos(x) x Sine(y)

Sine (x-y) = Sine(x) x Cos(y) – Cos(x) x Sine(y)

Cos (x y) = Cos(x) x Cos(y) – Sine(x) x Sine(y)

Cos (x-y) = Cos(x) x Cos(y) Sine(x) x Sine(y)

Tan (x y) = [Tan(x) Tan(y)] / [1-Tan(x) x Tan(y)]

Tan(x-y) = [Tan(x) -Tan(y)] / [1 Tan(x) x Tan(y)]

Conclusion

Trigonometry can be one of the most interesting topics you will ever learn, only if you make an effort to understand it. It can be made interesting if you remember these key points:

All right-angled triangles will always maintain the fixed ratio between the sides and the angles.
In all right-angled triangles, the square of the hypotenuse is always equal to the sum of the squares of the two other sides.
All similar right-angled triangles will maintain the proportional difference between each other.
Pythagoras Theorem could be applied to any right-angled triangle.
Trigonometry is an interesting subject.

As long as you keep these in mind, trigonometry will indeed be a breeze for you!